espiral Graceli quadrimensional e ou invertida

segunda-feira, 14 de julho de 2014

a lamniscata Graceli

g g g g g g

[x + y ] = g a [x - y ]

A lemniscata também pode ser descrita pelas coordenadas polares abaixo,

g g θ

r = a cos 2

pela respectivas coordenadas bipolares,

r r` = a / x

ou pela equação paramétrica:

g = Símbolo matemático Graceli que representa um número de uma sequência de números, escolhidos nas funções:

Logx/x [n] = g

Pi / x =

E outros.

Exemplo . logx/x = g

Onde x = 81

3/81 =
g = 0,037037037037037037

Logx/x [n] = g

g = 3/9 = 0,33333333333333333

Ou seja, g pode ser qualquer número, ou seja, é uma variável.

Logx/x [n] * pP

Logx/x [n] * pP * [a, R,0]. E outros.

Como funções de raiz. Ou mesmo x/ pi.

sábado, 12 de julho de 2014

geometria Graceli de espiral variável em relação a fluxos e ao tempo.

imagine uma lingua-de-cobra que se abre e se fecha em relação ao tempo.

espiral Graceli com sequências.

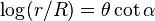
\, \log ( r / R ) = \theta \cot \alpha

1 ] r = logx/x [n] /t

2] r = logx/x [n] * pP /t

3] r = logx/x [n] * pP * Φ /t

4] r = logx/x [n] * pP * Φ /t * [a, R,0]

[a, R,0] = anternância entre reais e zero]

espiral invertida com elementos quadrimensional.

*θ * pP * logx/x [n] /t * * Φ

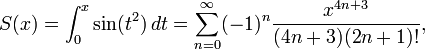S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},

+ *θ * pP * logx/x [n] /t *
* Φ

{C(x), S(x)} (Note que a espiral converge para o centro dos buracos na imagem acima conforme x tenta a infinito e a menos infinito.)

Seguindo a curva, o comprimento da curva de {S(0), C(0)} a {S(x), C(x)} deve ser igual a x, já que S′(x)² + C′(x)² = 1. O comprimento total da curva (de x = −∞ para ∞) é portanto infinito..

C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.

*θ * pP * logx/x [n] /t *

* Φ

\, \log ( r / R ) = \theta \cot \alpha

*θ * pP / t

Que resulta de sua expressão analítica nas coordenadas polares r e θ:

\, r ( \theta ) = R e^ { \theta cot \alpha }

* θ * pP./ t

pP= PROGRESSÃO COM EXPOENTE DE PROGRESSÃO.

\, \log ( r / R ) = \theta \cot \alpha

*θ * pP * logx/x [n] /t

Que resulta de sua expressão analítica nas coordenadas polares r e θ:

\, r ( \theta ) = R e^ { \theta cot \alpha }

* θ * pP./ t * logx/x [n] /t

\, \log ( r / R ) = \theta \cot \alpha

*θ * pP * logx/x [n] /t

Que resulta de sua expressão analítica nas coordenadas polares r e θ:

\, r ( \theta ) = R e^ { \theta cot \alpha }

* θ * pP./ t * logx/x [n] /t *

\, \log ( r / R ) = \theta \cot \alpha

*θ * pP * logx/x [n] /t * * Φ

Que resulta de sua expressão analítica nas coordenadas polares r e θ:

\, r ( \theta ) = R e^ { \theta cot \alpha }

* θ * pP./ t * logx/x [n] /t * * Φ

Φ = fluxos.

onde R é o raio associado a θ=0. Esta expressão apresenta a distância à origem, O, de um ponto da curva em função de θ.

com o ângulo crescente progressivamente chega a um ponto que a espiral se torna reta [com 180 graus] e chega a inverter a sua forma.