
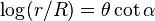 * *θ * pP / t
* *θ * pP / t
Que resulta de sua expressão analítica nas coordenadas polares r e θ:
 * * θ * pP./ t
* * θ * pP./ t
- pP= PROGRESSÃO COM EXPOENTE DE PROGRESSÃO.
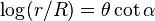 * *θ * pP * logx/x [n] /t
* *θ * pP * logx/x [n] /t * * θ * pP./ t * logx/x [n] /t
* * θ * pP./ t * logx/x [n] /t
Que resulta de sua expressão analítica nas coordenadas polares r e θ:
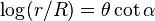 * *θ * pP * logx/x [n] /t
* *θ * pP * logx/x [n] /t * * θ * pP./ t * logx/x [n] /t *
* * θ * pP./ t * logx/x [n] /t * 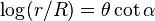 * *θ * pP * logx/x [n] /t *
* *θ * pP * logx/x [n] /t *  * * θ * pP./ t * logx/x [n] /t *
* * θ * pP./ t * logx/x [n] /t *
Que resulta de sua expressão analítica nas coordenadas polares r e θ:
Que resulta de sua expressão analítica nas coordenadas polares r e θ:
- Φ = fluxos.
- onde R é o raio associado a θ=0. Esta expressão apresenta a distância à origem, O, de um ponto da curva em função de θ.
- com o ângulo crescente progressivamente chega a um ponto que a espiral se torna reta [com 180 graus] e chega a inverter a sua forma.
Nenhum comentário:
Postar um comentário