sábado, 12 de julho de 2014


espiral invertida com elementos quadrimensional.



 *θ * pP * logx/x [n] /t * 
* Φ


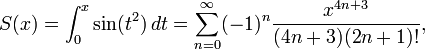S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},+  *θ * pP * logx/x [n] /t * 
* Φ




Cornu spiral.png



{C(x), S(x)} (Note que a espiral converge para o centro dos buracos na imagem acima conforme x tenta a infinito e a menos infinito.)
Seguindo a curva, o comprimento da curva de {S(0), C(0)} a {S(x), C(x)} deve ser igual a x, já que S′(x)² + C′(x)² = 1. O comprimento total da curva (de x = −∞ para ∞) é portanto infinito..



C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}. *θ * pP * logx/x [n] /t * 
* Φ








Postado por às

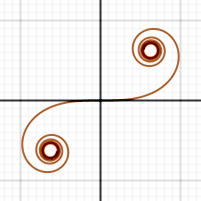
Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)